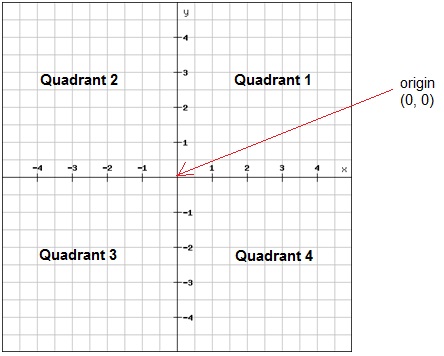
Given a coordinate plane, with 2 dimisions, it is natural to divide the plane in half and then in half again along each of the axis. As a result, there are 4 quarters, or "quadrants".

If the horizontal axis is "X" and the vertical is "Y" then yhe values of X or Y will be positive or negative in each quadrant as shown in this table:
| Quadrant | X | Y |
| 1 "I" | + | + |
| 2 "II" | - | + |
| 3 "III" | - | - |
| 4 "IV" | + | - |
The magnatude or size without sign, will be increasing in the directions indicated in this table
| Quadrant | X | Y |
| 1 "I" | right | up |
| 2 "II" | left | up |
| 3 "III" | left | down |
| 4 "IV" | right | down |
So, if we are "in the 4th quadrant" then the X value will be increasing as we move right and the Y value will be "increasing" (if we dont look at the sign) as we move down.
For example: The point x=1, y=-1 is right and down from the origin. x=2, y=-2 is further right and down. So as the magnitude of the numbers inreases, we are moving right and down. We could represent that as "x=2, y=2 in the 4th quadrant" and it should be understood that y is actually -2.
In each quadrant, we notice that different types of trig fuctions will be positive or negative. For example, in Quadrant 1, all the trig fuctions, sin, cosecant, cosine, secant, tangent, and cotangent are all positive. In the 3rd quadrant, only the tangent and cotangent are positive. The menomic "All Science Teachers Crazy" can help to remember which set of trig functions are positive in each quadrant.
| Quadrant II "Science" + SIN, COSEC - COS, SEC - TAN, COTAN |
Quadrant I "All" + SIN, COSEC + COS, SEC +TAN, COTAN |
| Quadrant III "Teachers" - SIN, COSEC - COS, SEC +TAN, COTAN |
Quadrant IV "Crazy" - SIN, COSEC + COS, SEC - TAN, COTAN |