A simple transistor model is given by 
.
A more general model capable of describing the family of
characteristic curves is given by
where 
is a transistor-dependent function.
For AC analysis only time changes are important and we may write
where the partial derivatives are evaluated at a particular
and 
- the operating point.
is the
forward current transfer ratio and describes the vertical spacing
between the curves.
The output admittance (inverse resistance) is 
and describes the slope 
of one of the curves as it passes through the
operating point.
Using these definitions we may write
The input signal 
is also related to and , and
a similar argument to the above gives
where 
is the input impedance and 
is the reverse
voltage ratio.
The differential equations are linear only in the limit of small AC
signals, where the h parameters are effectively constant.
The h parameters are in general functions of the variables and
.
We arbitrarily picked and as our independent variables.
We could have picked any two of 
and .
Because the current and voltage variables are mixed the h parameters
are known as hybrid parameters.
In general the current and voltage signals will have both DC and AC components. The time derivatives involve only the AC component and if we restrict ourselves to sinusoidal AC signals, we may replace the time derivatives by the signals themselves (using complex notation). Our hybrid equations become
The hybrid parameters are often used as the manufacturer's specification of a transistor, but there are large variations between samples. Thus one should use the actual measured parameters in any detailed calculation based on this model. Table 5.2 shows typical values for the hybrid parameters.
The relationship between the voltages and currents for a transistor in the common emitter configuration is shown in figure 5.6.
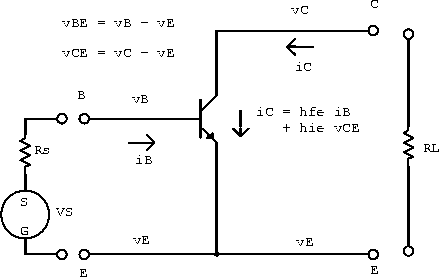
Figure 5.6: Transistor in the common emitter configuration.
We now make a few approximations to our hybrid parameter model to get an intuitive feel for how transistors behave in circuits. The voltage across the load resistor is
Substituting this into our first hybrid equation gives
If 
(good to about 10%) we can write
which is the AC equivalent of 
.
Similarly, using the second hybrid equation gives
If 
(good to about 10%) we have
which is the AC voltage gain.
